For example if a problem requires you to divide by a fraction you can more easily multiply by its reciprocal.
3x3 matrix adj a formula.
This is an inverse operation.
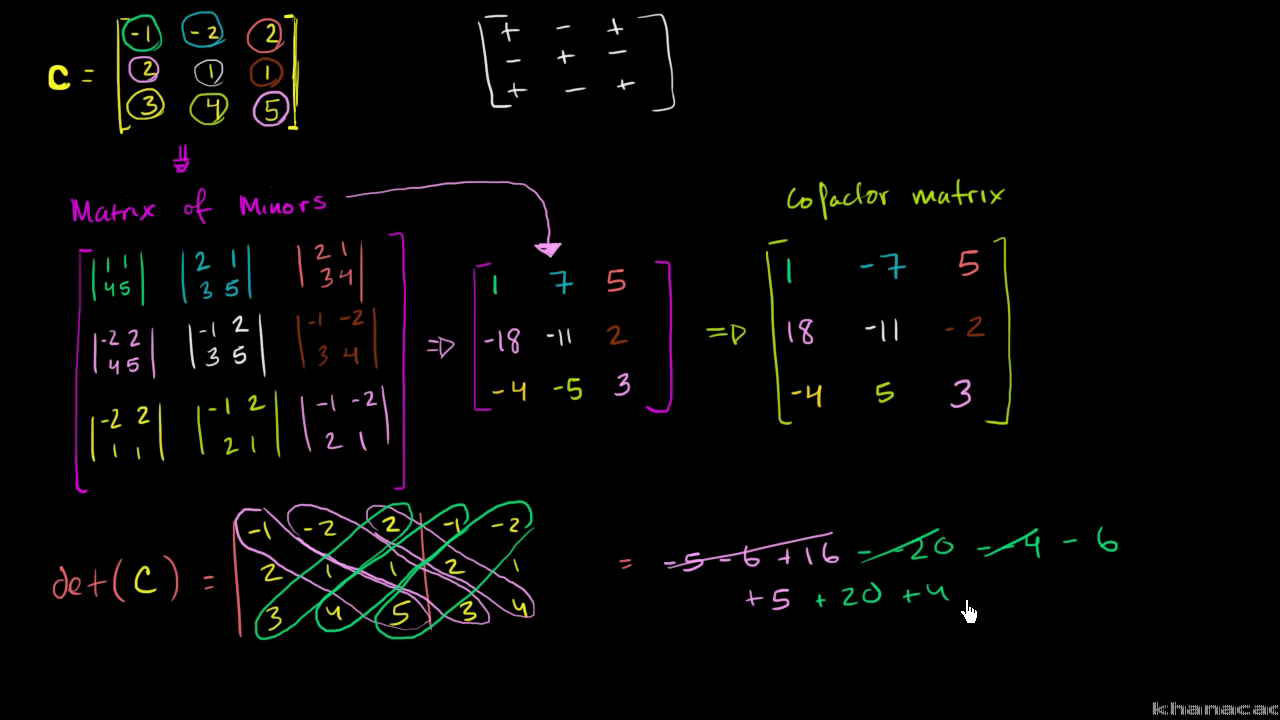
Inverting a 3x3 matrix using determinants part 1.
A singular matrix is the one in which the determinant is not equal to zero.
This is the currently selected item.
Inverse of a 3x3 matrix.
Matrices when multiplied by its inverse will give a resultant identity matrix.
Similarly since there is no division operator for matrices you need to multiply by the inverse matrix.
Port 1 input matrix 3 by 3 matrix.
In the past the term for adjugate used to be adjoint.
In the below inverse matrix calculator enter the values for matrix a and click calculate and calculator will provide you the adjoint adj a determinant a and inverse of a 3x3 matrix.
The name has changed to avoid ambiguity with a different defintition of the term adjoint.
Calculating the inverse of a 3x3 matrix by hand is a tedious job but worth reviewing.
The adjugate of a is the transpose of the cofactor matrix c of a.
To find the inverse of a 3 by 3 matrix is a little critical job but can be evaluated by following few steps.
The adjoint of 3x3 matrix block computes the adjoint matrix for the input matrix.
The following relationship holds between a matrix and its inverse.
For related equations see algorithms.
Solving equations with inverse matrices.
The matrix adj a is called the adjoint of matrix a.
A 3 x 3 matrix has 3 rows and 3 columns.
Elements of the matrix are the numbers which make up the matrix.
When a is invertible then its inverse can be obtained by the formula given below.
Let s consider the n x n matrix a aij and define the n x n matrix adj a a t.
The adjugate of matrix a is often written adj a.
3x3 identity matrices involves 3 rows and 3 columns.
Inverting a 3x3 matrix using determinants part 2.
The inverse is defined only for non singular square matrices.
In more detail suppose r is a commutative ring and a is an n n matrix with entries from r the i j minor of a denoted m ij is the determinant of the n 1 n 1 matrix that results from deleting row i and column j of a the cofactor matrix of a is the n n matrix c whose i j entry is the.